3 Disc. Sim. of Cont. Systems

In a direct realization, the computer code implementing the different equation closely follows the form of the difference equation

$$y_k = a_1y_{k−1} + a_2y_{k−2} \optbreak{}+ b_0u_k + b_1u_{k−1} + b_2u_{k−2}$$

This is demonstrated in the code fragment shown below. The code fragment is written in C and is designed to run under freeRTOS, a free real-time operating system.

Block Diagram
Figure 1: Schematic of system used to implement a different equation.
01 // start of code fragment
02float a1 = 0.0, a2 = -0.1716; // initialize transfer
03float b0 = 0.2929, b1 = 0.5858, b2 = 0.2929; // function coefficients
04float y[3] = {0,0,0}; // initialize y values
05float u[3] = {0,0,0}; // initialize u values
06long int xLastWakeTime = xTaskGetTickCount();
07int Ts = 5; // sampling time in milliseconds
08while (1) { // loop forever
09u[0] = adc_in(); //Read input u(k)
10y[0] = a1*y[1] + a2*y[2] + b0*u[0] + b1*u[1] + b2*u[2]; // compute y[k] using direct realization
11dac_out(y[0]); // Write output y(k) to D/A converter
12u[2] = u[1]; // Propagate variables
13u[1] = u[0];// backwards
14y[2] = y[1]; // for next
15y[1] = y[0]; // sample
16vTaskDelayUntil(&xLastWakeTime,Ts)// wait until the time for the next sample
17}

Use the Input control to change the input to the system in Figure 1. Use Step to step through the code one line at a time. The highlighted line will be executed after pressing Step The current value of the variables are shown as Variable Value.

Variable Values: u[0]=0.00
u[1]=0.00
u[2]=0.00 y[0]=0.00
y[1]=0.00
y[2]=0.00
  1. What is the purpose of the code that starts in line 12?
  2. How many multiplication and additions must be implemented from the time the signal is read from the ADC to when it is outputs the value of $y_k$ at the DAC?
  3. How many multiplication and additions must be implemented from the time the signal is read from the ADC to when it is outputs the value of $y_k$ at the DAC if the code implemented a 3rd order difference equation.

 

In the code above the difference equation is explicitly calculated in line 10. While this approach is easy to follow, there is a potentially large computational delay between the acquisition of the input sample in line 09 and the writing of the output sample in line 11.

Also note the possibility of clock overrun in the line 16. If the code takes longer to execute than the sample time, Ts, the time allotted for the control computation is too short.

Consider the block diagram shown in Figure 2. Input $u$ and output $y$ are present, as are parameters $a_k$ and $b_k$.

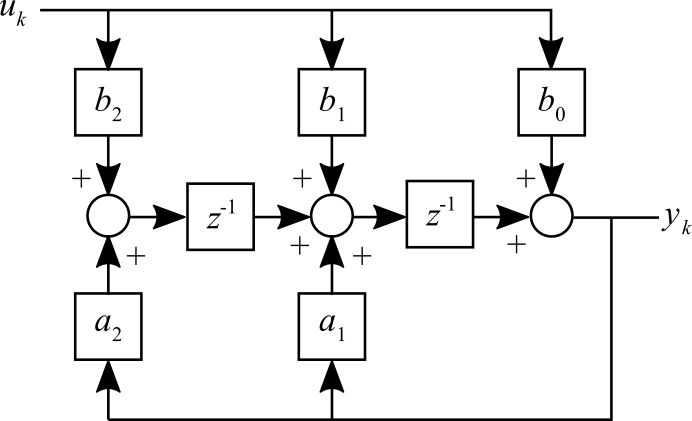
Observer canonical block diagram realization
Figure 2: Observer canonical block diagram realization

The computer code implementing the different equation using cannonical form is shown below. The code fragment is written in C and is designed to run under freeRTOS, a free real-time operating system.

Block Diagram
Figure 3: Schematic of system used to implement a different equation.
01 // start of code fragment
02float a1 = 0.0, a2 = -0.1716; // initialize transfer
03float b0 = 0.2929, b1 = 0.5858, b2 = 0.2929; // function coefficients
04float y = 0, u = 0; // initialize y and u values
05float x1 = 0, x2 = 0; // initialize state values
06long int xLastWakeTime = xTaskGetTickCount();
07int Ts = 5; // sampling time in milliseconds
08while (1) { // loop forever
09u = adc_in(); //Read input u(k)
10y = x1 + b0*u; // compute y using cannonical realization
11dac_out(y); // Write output y(k) to D/A converter
12x1 = x2 + b1*u + a1*y; // Propagate variables
13x2 = b2*u + a2*y;// backwards
14vTaskDelayUntil(&xLastWakeTime,Ts)// wait until the time for the next sample
15}

Use the Input control to change the input to the system in Figure 3. Use Step to step through the code one line at a time. The highlighted line will be executed after pressing Step The current value of the variables are shown as Variable Value.

Variable Values: y=0.00
u=0.00
 x1=0.00
x2=0.00
  1. How many multiplication and additions must be implemented from the time the signal is read from the ADC to when it is outputs the value of $y_k$ at the DAC? Compare that to line 10 in the direct realization.
  2. How many multiplication and additions must be implemented from the time the signal is read from the ADC to when it is outputs the value of $y_k$ at the DAC if the code implemented a 3rd order difference equation - speculate.
  3. Where would quantization error occur in this system?

 

Although the program loop is shorter overall, note particularly that the computational delay between line 09 and line 11 is much shorter (see the activity questions) There is more computation after writing the output, but it’s not as critical there.